(SOLVED) Outer Product
Discipline: Mathematics
Type of Paper: Question-Answer
Academic Level: Undergrad. (yrs 3-4)
Paper Format: APA
Pages: 1
Words: 275
Question
The tensor product of two coordinate vectors is termed as “Outer
product”. This is a special case for “Kronecker product of matrices”.
Let u and v be vectors. Then, the outer product of u and v is w=uvT. The outer product 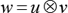 is same as the matrix multiplication uvT also u is denoted by m × 1 column vector and v is denoted by n × 1 column vector.
is same as the matrix multiplication uvT also u is denoted by m × 1 column vector and v is denoted by n × 1 column vector.
Let
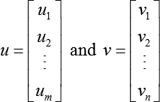 be two vectors. Then, the outer product of u and v is obtained as follows:
be two vectors. Then, the outer product of u and v is obtained as follows:
Properties of an outer product:
• The result of an outer product is m × n rectangular matrix.
• The outer product is not commutative. That is,
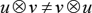
• Multiply the second vector v with the resultant product
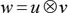 gives a vector of the first factor u scaled by the square norm of the second factor v. That is,
gives a vector of the first factor u scaled by the square norm of the second factor v. That is,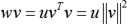
Example:
Consider the vectors
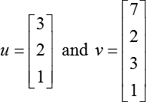 .
.Transpose of v is, vT = [7 2 3 1].
The outer product of
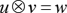 , which is obtained below:
, which is obtained below: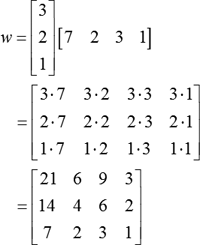
Thus, the outer product is a rectangular 3 × 4 matrix.
Check the outer product is commutative or not.
